
문제 링크 : https://www.acmicpc.net/problem/1389
이 문제는 전형적인 플로이드 워셜 알고리즘을 이용하여 해결할 수 있는 문제이다.
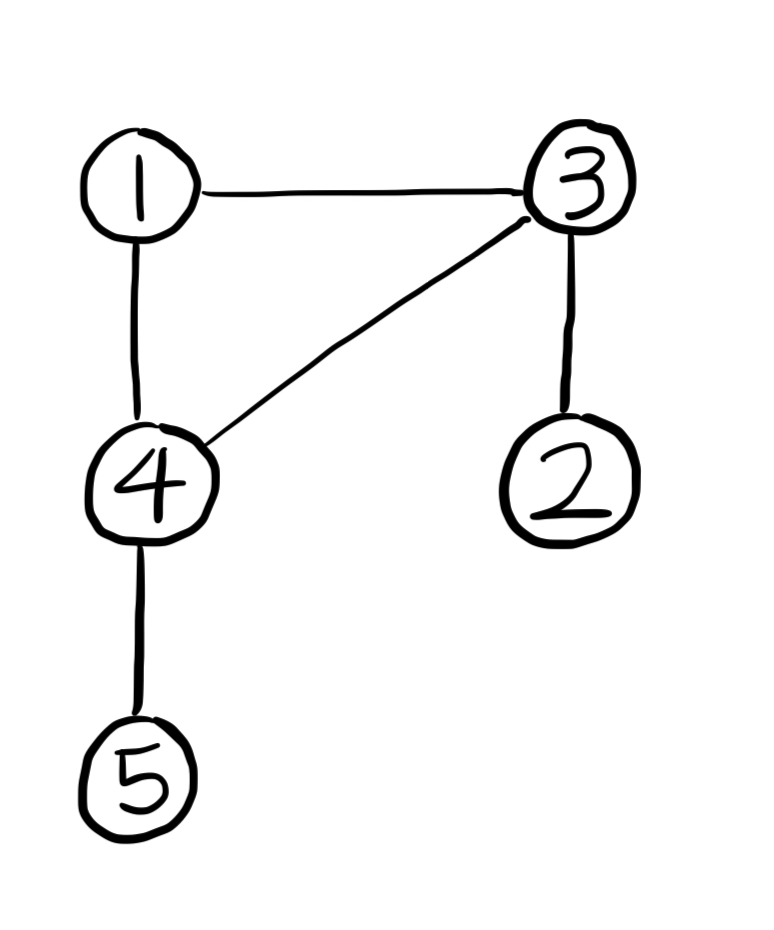
예제 입력을 그래프로 표현하면 위와 같다. 여기서 단방향이 아니라는 것에 주의해서
거리 배열을 초기화한다.

거리배열을 초기화하면 인접 정점끼리의 관계를 표현할 수 있다.
여기서 무한대는 문제의 조건을 보고 직접 적당히 큰 값을 넣거나,
아니면 Interger.MAX_VALUE와 같이 int 범위에서 가장 큰 값을 넣어주면 된다.
다만 이럴 경우에는 연산의 과정에서 int의 범위를 넘어 오버플로우가 발생할 수 있기 때문에
long 타입으로 캐스팅한 후에 연산을 해줘야 한다.
거리배열을 초기화한 후에는 플로이드 워셜 알고리즘으로 각 정점사이의 최단거리를 구해주고
1번부터 N번까지 중 배열의 합이 가장 작은 번호를 고르면 되는데,
이때 문제의 조건에 맞게 낮은 번호부터 순회하여 골라준다.
package boj;
import java.util.*;
import java.io.*;
public class BOJ1389 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[][] arr = new int[N+1][N+1];
for(int i = 1; i <= N; i++){
for(int j = 1; j <=N; j++){
if(i != j) arr[i][j] = Integer.MAX_VALUE;
}
}
for(int i = 0; i < M; i++){
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
arr[u][v] = 1;
arr[v][u] = 1;
}
for(int k = 1; k <= N; k++){
for(int i = 1; i <= N; i++){
for(int j = 1; j <= N; j++){
arr[i][j] = (int) Math.min((long) arr[i][j], ((long) arr[i][k] + arr[k][j]));
}
}
}
int min = Integer.MAX_VALUE;
int idx = 0;
for(int i = 1; i < arr.length; i++){
int sum = Arrays.stream(arr[i]).sum();
if(min > sum){
min = sum;
idx = i;
}
}
System.out.println(idx);
}
}
'PS' 카테고리의 다른 글
| [BOJ][Java] 17472번 다리 만들기 2 (0) | 2025.03.06 |
|---|---|
| [BOJ][Java] 1197번 최소 스패닝 트리 (0) | 2025.03.05 |
| [BOJ][Java] 11403번 경로 찾기 (0) | 2025.03.04 |
| [BOJ][Java] 11404번 플로이드 (0) | 2025.03.04 |
| [BOJ][Java] 11657번 타임머신 (1) | 2025.03.03 |