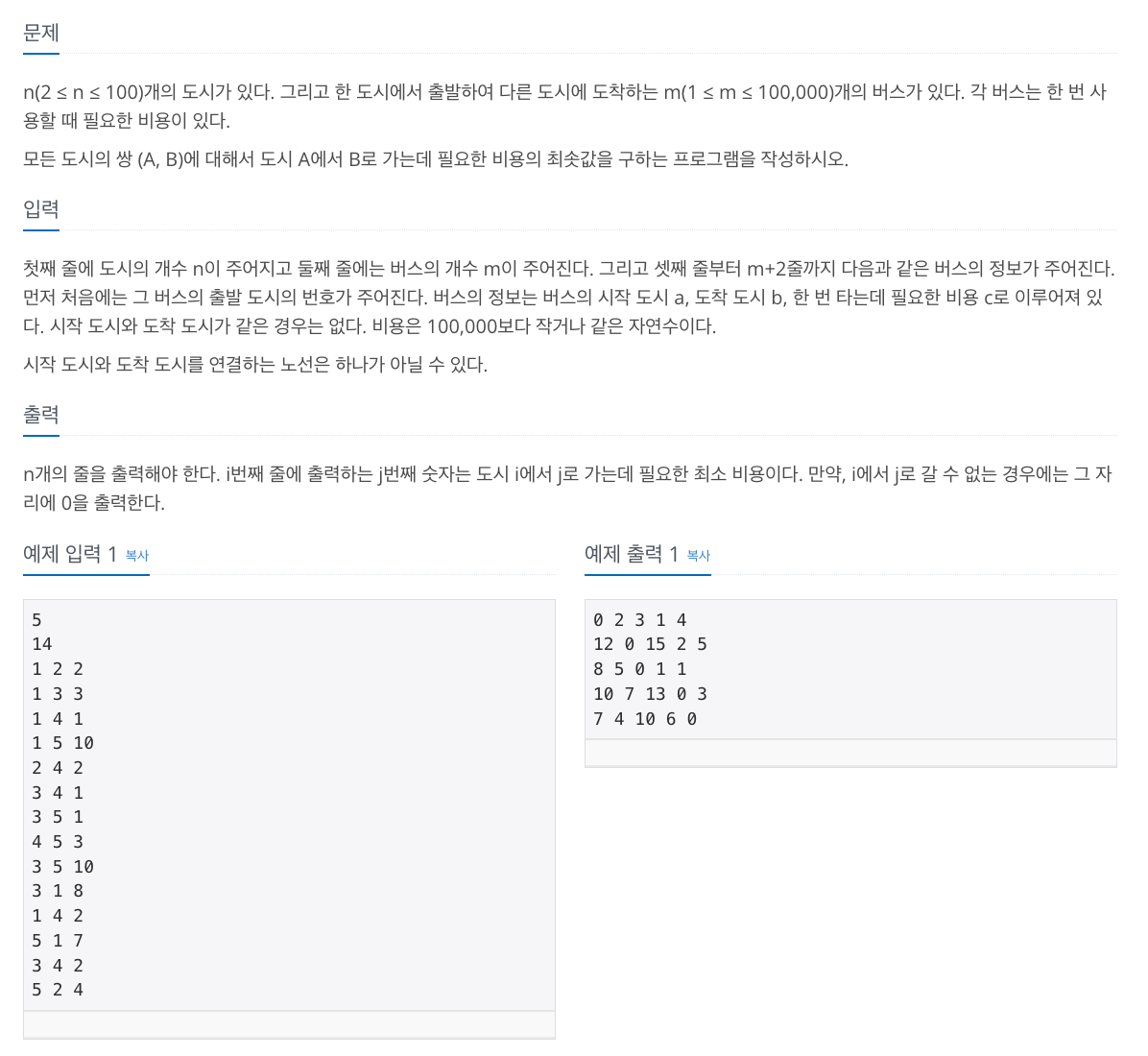
문제 링크 : https://www.acmicpc.net/problem/11404
문제의 이름이 플로이드인 만큼 플로이드-워셜 알고리즘을 사용하는 문제이다.
플로이드 워셜 알고리즘은 모든 정점사이 간의 최단거리를 알아내는 알고리즘으로
정점의 개수가 N 이라고 했을 때 시간복잡도가 O(N^3)인 알고리즘이다.
따라서 플로이드 워셜 알고리즘을 사용하는 문제는 정점의 개수인 N이 작다는 특징이 있다.

우선 플로이드 워셜 알고리즘을 구현하기 위해 인접 행렬을 만들어주고
값을 채워준다. 여기서 값이 의미하는 것은 arr[S][E] 는 정점 S부터 정점 E 까지 가는데 드는 최소비용이라는 의미이다.
여기서 S와 E가 동일하다면 움직이지 않는것을 의미하기 때문에 0으로 초기화해준다.

그리고 3중 for문을 이용해서 위의 점화식을 수행하면 된다.
이때 주의 사항으로는 만약 arr배열에서 무한대로 표시한 곳에 최댓값을 계산해서 넣지 않고
Integer.MAX_VALUE와 같이 Integer의 최댓값을 넣었다면 long 타입으로 캐스팅한 후 위의 점화식을 실행해야 한다.
package boj;
import java.util.*;
import java.io.*;
public class BOJ11404 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int n = Integer.parseInt(br.readLine());
int m = Integer.parseInt(br.readLine());
int[][] arr = new int[n+1][n+1];
for(int i = 1; i < arr.length; i++){
for(int j = 1; j < arr.length; j++){
if(i == j) continue;
arr[i][j] = Integer.MAX_VALUE;
}
}
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
if(arr[u][v] > w){
arr[u][v] = w;
}
}
for(int k = 1; k <= n; k++){ // 경유 정점
for(int s = 1; s <= n; s++){ // 출발 정점
for(int e = 1; e <=n; e++){ // 도착 정점
arr[s][e] = (int) Math.min((long)arr[s][e], ((long)arr[s][k] + arr[k][e]));
}
}
}
StringBuilder sb = new StringBuilder();
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
if(arr[i][j] == Integer.MAX_VALUE) sb.append(0).append(" ");
else sb.append(arr[i][j]).append(" ");
}
sb.append("\n");
}
System.out.println(sb);
}
}
'PS' 카테고리의 다른 글
| [BOJ][Java] 1389번 케빈 베이컨의 6단계 법칙 (0) | 2025.03.05 |
|---|---|
| [BOJ][Java] 11403번 경로 찾기 (0) | 2025.03.04 |
| [BOJ][Java] 11657번 타임머신 (1) | 2025.03.03 |
| [BOJ][Java] 1854번 K번째 최단경로 찾기 (0) | 2025.03.02 |
| [BOJ][Java] 1753번 최단경로 (0) | 2025.03.01 |