
문제 링크 : https://www.acmicpc.net/problem/11050
문제 자체는 매우 쉬운 문제이지만
조합을 구하는 방법을 익혀볼 수 있는 문제이다.
조합을 구하는 과정을 간단히 알아보면 아래와 같다.

조합의 수학적 정의는 위와 같고, 이는 n개 중에서 r개를 고르는데
이때 순서는 상관이 없다는 의미이다. (1,2,3 이나 3,2,1 이나 똑같다)
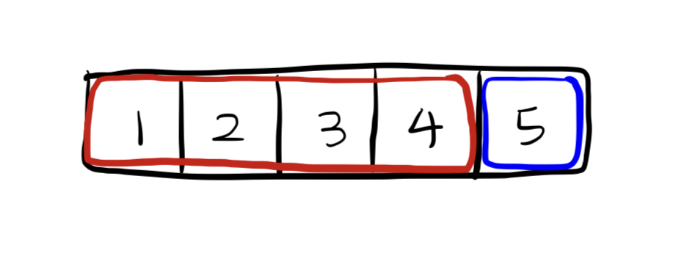
우선 5개의 숫자가 있고 5개중에서 4개를 고르는 경우는 이미 계산했다고 가정한다.
그렇게 5개중 4개를 골랐을 때 뽑힌 숫자가 1,2,3,4이다.
이제 5개 중에서 3개를 고르는 경우를 생각해보면 아래와 같은 경우의 수가 있다.

아직 선택되지 않은 5를 선택하고
5개 중 4개를 골랐을 때 선택된 1,2,3,4 중에 2개를 선택하는 경우

또는 5를 선택하지 않고
5개중 4개를 골랐을때 선택된 1,2,3,4 중에 3개를 선택하는 경우이다.

이를 점화식으로 표현해 보면 D[5][3] 5개 중에서 3개를 고르는 경우의 수는
D[4][2] + D[4][3] 4개 중 2개를 고르는 경우의 수 + 4개중 3개를 고르는 경우의 수
라고 정리할 수 있다.

이제 점화식을 일반화하면 위와 같은 공식을 구할 수 있다.
해당 점화식을 이용해 i개중 j개를 고르는 경우의 수를 계산할 수 있다.

생각해 보면 계산하지 않고도 위와 같은 경우는 이미 정답을 알고 있다.
i개중 i개를 고르는 경우의 수는 1이다.
i개중 0개를 고르는 경우의 수는 1이다.
i개중 1개를 고르는 경우의 수는 i이다.
위의 기본조건을 통해 2차원 배열에 초기화해주고
위에서 구한 점화식 D[i][j] = D[i-1][j-1] + D[i-1][j] 를 사용하면 모든 조합을 구할 수 있다.
package boj;
import java.util.*;
import java.io.*;
public class BOJ11050 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[][] arr = new int[N+1][N+1];
for(int i = 0; i <= N; i++){
arr[i][1] = i;
arr[i][i] = 1;
arr[i][0] = 1;
}
for(int i = 1; i < arr.length; i++){
for(int j = 0; j < arr.length; j++){
if(arr[i][j] == 0) arr[i][j] = arr[i-1][j] + arr[i-1][j-1];
}
}
System.out.println(arr[N][K]);
}
}
'PS' 카테고리의 다른 글
| [BOJ][Java] 2193번 이친수 (0) | 2025.03.13 |
|---|---|
| [BOJ][Java] 1991번 트리 순회 (1) | 2025.03.08 |
| [BOJ][Java] 1068번 트리 (0) | 2025.03.07 |
| [BOJ][Java] 11725번 트리의 부모 찾기 (1) | 2025.03.07 |
| [BOJ][Java] 1414번 불우이웃돕기 (0) | 2025.03.06 |