
문제 링크 : https://www.acmicpc.net/problem/1717
해당 문제는 유니온 파인드의 대표유형 같은 문제이다.
예제를 따라가며 유니온 파인드를 구현해보자.
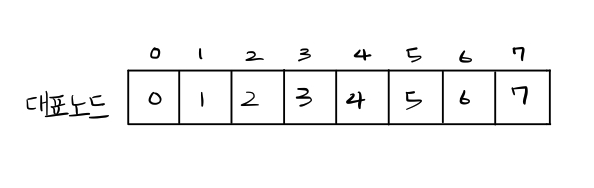
먼저 예제에 나온 대로 0부터 7까지의 노드가 있다고 할 때
각각 자신이 속한 집단의 대표노드가 된다.
그럼 위와 같이 n+1 개의 집합으로 초기화된다.

첫 번째 입력값인 0 1 3을 받았을 때는 1과 3이 속한 집합을 하나로 합쳐야 한다.
초기에는 1과 3번 노드 집합의 대표노드가 각각 1과 3이므로 3의 대표집합을 1로 변경해 주면 된다.
그다음 입력값인 1 1 7은 1번과 7번이 같은 집합임을 묻는데 확인해 보면 서로
대표 노드가 다르므로 NO를 출력해 주면 된다.

다음 입력인 0 7 6도 마찬가지로 각각의 노드가 속한 집합의 대표노드가
자기 자신이므로 6번 노드의 대표노드를 7로 변경했다.
그다음 입력값인 1 7 1도 확인해 보면 서로 대표노드가 다르므로 NO를 출력해 주면 된다.

잠시 예제에서 벗어나서 파인드 연산에 대해 알아보면
예제를 따라 집합을 합치다 보면 위처럼 5번 노드가 자신의 집합의 대표노드라고
적힌 4번이 실제 대표노드가 아닌 경우가 생긴다.
만약 이런 상태로 대표노드를 찾는다면 5번의 대표노드를 찾기 위해서는
5 -> 4 -> 3 -> 2 -> 1 (대표 노드) 이런 식으로 연산의 길이가 길어지게 된다.
이런 것을 방지하려면 경로 압축을 해줘야 하는데
경로 압축이란 위에 그림에서 3,4,5번 노드가 속한 집합의 실제 대표노드인
1번 노드로 변경하는 방식이다.
이렇게 하면 추후 특정 노드가 속한 대표집합을 찾을 때 O(1)의 시간복잡도로
찾을 수 있어 해당 문제처럼 input값이 큰 경우에도 실행시간을 크게 줄일 수 있다.
package boj;
import java.util.*;
import java.io.*;
public class BOJ1717 {
static int[] heads;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
heads = new int[n+1];
for(int i = 0; i < heads.length; i++){
heads[i] = i;
}
StringBuilder sb = new StringBuilder();
for(int i = 0; i < m; i++){
st = new StringTokenizer(br.readLine());
int uf = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
if(uf == 0){
union(a,b);
}else{
int aHead = find(a);
int bHead = find(b);
if(aHead == bHead) sb.append("YES\n");
else sb.append("NO\n");
}
}
System.out.println(sb);
}
static void union(int a, int b){
int aHead = find(a);
int bHead = find(b);
if(aHead != bHead){
heads[bHead] = aHead;
}
}
static int find(int n){
if(n == heads[n]) return n;
return heads[n] = find(heads[n]);
}
}'PS' 카테고리의 다른 글
| [BOJ][Java] 1043번 거짓말 (0) | 2025.02.26 |
|---|---|
| [BOJ][Java] 1976번 여행 가자 (0) | 2025.02.26 |
| [BOJ][Java] 1707번 이분 그래프 (0) | 2025.02.25 |
| [BOJ][Java] 18352번 특정 거리의 도시 찾기 (0) | 2025.02.24 |
| [BOJ][Java] 1850번 최대공약수 (0) | 2025.02.20 |